A factor is a number that will divide exactly into another number. For example, 8 is a factor of 24 because 8 will fit into 24 exactly 3 times with no remainder.
Factor pairs are two numbers which multiply together to make a particular number. For example, the factor pairs of 12 are 1 and 12; 2 and 6; 3 and 4. This means that the factors of 12 (in order) are 1, 2, 3, 4, 6 and 12. Writing factors in pairs helps to avoid missing out any important numbers.
Example
List all the factors of 24.
The smallest number that will divide exactly into 24 is 1. Remember, 1 is a factor of every whole number (
integer). 1 will divide into 24 exactly 24 times (because

) so 24 is the factor pair that fits with 1.
Once the first factor pair has been recorded, move onto the next biggest number, 2, and consider whether this will divide into 24 or not. 2 will divide into 24 exactly 12 times, so 2 and 12 are factor pairs.
Keep considering each number in turn and whether it will divide into 24 or not. If so, write it as a factor pair in the list.
All factor pairs will have been found when the next number to consider is already in the list.
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24.
Multiples
A multiple of a number is any number that can be divided exactly by that number.
For example, the multiples of 5 are all of the numbers that 5 will divide into, which is essentially the 5 times tables. The multiples of 5 are 5, 10, 15, 20, 25 and so on.
The multiples of numbers are
infinite.
Prime numbers
A prime number is a number which is only divisible by 1 and itself. Another way to think of prime numbers is that they are only ever found as answers in their own times tables.
11 is a prime number because the only factors of 11 are 1 and 11 (

). No other whole numbers can multiply together to make 11.
9 is not a prime number because the factors of 9 are 1, 3 and 9 (

,

). There is more than one way to make the number 9 so it is not a prime.
1 is not a prime number as it only has one factor - itself.
There are an infinite number of prime numbers. Prime numbers under 30 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.
Powers
Powers, or
indices, are ways of writing numbers that have been multiplied by themselves:
 can be written as 22 (2 squared)
can be written as 22 (2 squared)  can be written as 23 (2 cubed)
can be written as 23 (2 cubed)  can be written as 24 (2 to the power of 4), and so on
can be written as 24 (2 to the power of 4), and so on
The small floating digit is known as the power or index number.
Roots are the opposite of powers. If 2 squared is 4, then the square root of 4 must be 2.

. Reversing this gives

.

terms can be collected together to give
.
.
 simplified is
simplified is 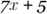 .
.terms.
can be simplified to
